?全國2013年1月高等教育自學考試《高等數學(一)》試題
摘要:本試卷為2103年1月自考高等數學真題,總分100分,測試時間150分鐘;包含詳細試題解析。
本試卷為2103年1月自考高等數學真題,總分100分,測試時間150分鐘;包含詳細試題解析。
一、單項選擇題(每小題2分,共10分)
1.設函數![]() ,則f(x)=
,則f(x)=
A.x(x+1)
B.x(x-1)
C.(x+1)(x-2)
D.(x-1)(x+2)
3.設函數![]() ,則高階導數
,則高階導數![]() =
=
A.12!
B.11!
C.10!
D.0
2.若x→0時函數f(x)為x^2的高階無窮小量,則![]() =
=
A.0
B.1/2
C.1
D.∞
4.曲線![]()
A.僅有鉛直漸近線
B.僅有水平漸近線
C.既有水平漸近線又有鉛直漸近線
D.無漸近線
5.設函數f(x)連續,![]() ,則
,則![]() =
=
A.xf(x)
B.af(x)
C.-xf(x)
D.-af(x)
二、填空題(每小題3分,共30分)
1.設函數![]() ,則f(x)的定義域為__________.
,則f(x)的定義域為__________.
3.某商品需求量Q與價格P的函數關系為Q=150-2P^2,則P=6時的邊際需求為__________.
6.極限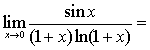 __________.
__________.
2.極限![]() =_________.
=_________.
10.設函數z=![]() ,則
,則![]() =__________.
=__________.
4.函數![]() 在區間[0,1]上滿足拉格朗日中值定理的中值ζ=__________.
在區間[0,1]上滿足拉格朗日中值定理的中值ζ=__________.
9.若![]() ,則f(x)=__________.
,則f(x)=__________.
8.微分方程![]() 的通解為__________.
的通解為__________.
5.函數![]() 在區間[-1,1]上的最小值為__________.
在區間[-1,1]上的最小值為__________.
7.定積分![]() __________.
__________.
三、計算題(一)(每小題5分,共25分)
1.討論函數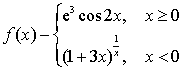 在x=0處的連續性.
在x=0處的連續性.
3.求不定積分![]() .
.
4.設函數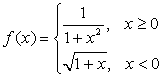 ,計算定積分
,計算定積分![]() .
.
2.設函數![]() ,求d y.
,求d y.
5.計算二重積分![]() ,其中區域D由曲線
,其中區域D由曲線![]() 及直線x=2圍成.
及直線x=2圍成. 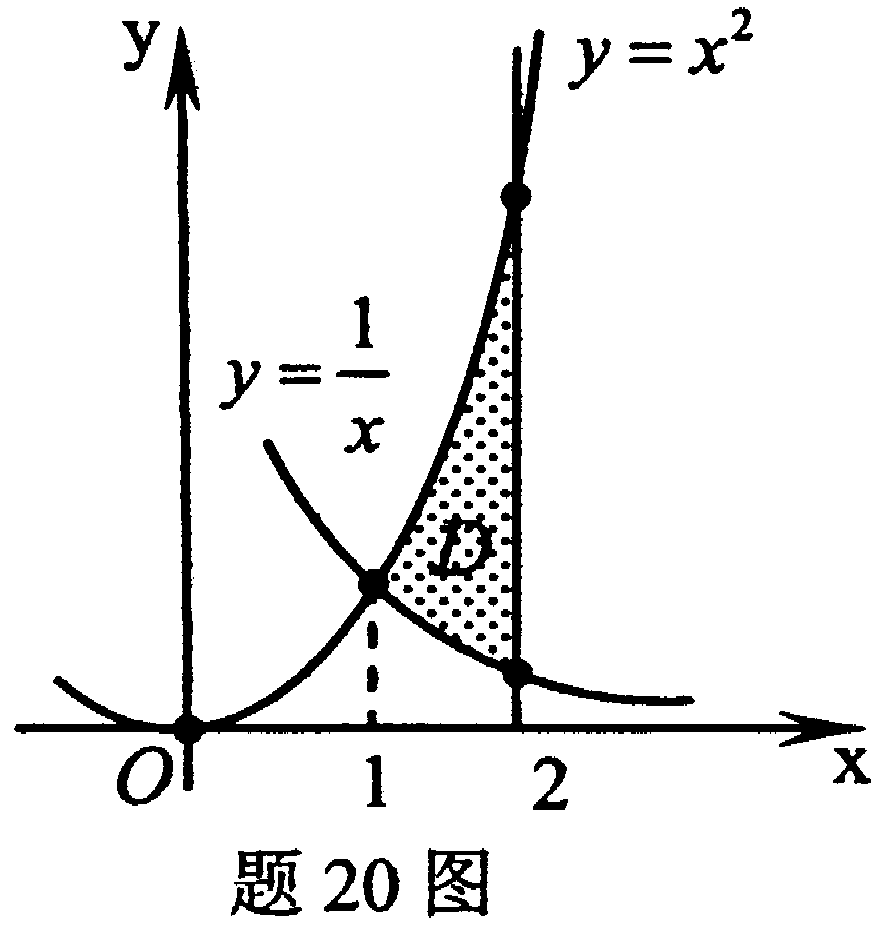
四、計算題(二)(每小題7分,共21分)
1.設函數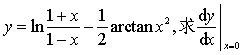 .
.
2.求曲線![]() 的凹凸區間及拐點.
的凹凸區間及拐點.
3.計算定積分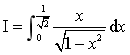 .
.
五、應用題(本題9分)
1.設某企業生產一定量的某產品時可用兩種原料,第一種為x(千噸),第二種為y(千噸),其電能消耗量N(萬度)與兩種原料使用量的關系為![]() 問如何使用兩種原料方可使電能消耗達到最低,并求此時的最低能耗.
問如何使用兩種原料方可使電能消耗達到最低,并求此時的最低能耗.
六、證明題(本題5分)
1.證明當x>0時,![]()
延伸閱讀
- 考前自救指南:希賽自考題庫快速提分
- 自考專屬刷題工具,刷題即提分!
- 最后9天,自考歷年真題應該怎么刷?
- 自考備考一站式服務:希賽自考題庫APP
- 0基礎逆襲秘籍:希賽全套自考學習包(含智能題庫)
- 避開備考誤區!用希賽自考APP快速提分!

自考微信公眾號

掃碼添加
自考備考資料免費領取
去領取











 掃描二維碼
掃描二維碼