2022年北京建筑大學專升本數學考試大綱

1. 函數

一元函數的定義;

函數的表示方法(包括分段函數);

函數的性質(有界性、單調性、奇偶性、周期性等);

函數的增量;

反函數;

復合函數;

基本初等函數與初等函數。

2. 極限與連續

數列與數列的極限的描述性定義;

收斂數列的簡單性質：有界性、唯一性等;

數列極限存在的單調有界準則;

函數極限(描述性)定義：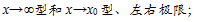

夾逼準則;

極限的四則運算;

兩個重要極限;

無窮小量與無窮大量的概念、無窮小量的比較;

無窮小量與無窮大量的關系;

函數極限與無窮小量的關系;

函數的連續性與間斷點;

連續函數的和、差、積、商的連續性;

初等函數的連續性;

閉區間上連續函數的性質：界值定理、最值定理及其應用。

3.導數與微分

導數的定義、導數的幾何意義;

導數作為函數對自變量的變化率的概念;

平面曲線的切線與法線;

函數可導與連續的關系;

函數的和、差、積、商的求導運算法則;

復合函數的求導法則;

反函數的求導法則;

基本初等函數的求導公式及初等函數的求導問題;

高階導數;隱函數求導法則、對數求導法;

由參數方程所確定的函數的求導方法;

微分的定義、基本公式、運算法則;

一階微分的形式不變性。

4. 微分學應用

微分中值定理：羅爾定理、拉格朗日定理、柯西定理。

羅比達法則;

函數的增減性的判定;

函數的極值及其求法;

函數的最大值、最小值及其應用;

曲線的凹向及其判定法;

拐點及其求法;

函數作圖;

弧微分。

5. 不定積分

原函數、不定積分的定義;

原函數、不定積分的幾何意義;

不定積分的基本性質;

基本積分公式;

換元積分法、分部積分法;

簡單有理函數和可化為簡單有理函數的積分法。

6. 定積分及其應用

定積分的定義及其存在定理;

定積分的基本性質;

定積分的中值定理;

微積分學的基本定理;

牛頓----萊布尼茨公式;

定積分的換元積分法、分部積分法;

積分區間為無限區間的廣義積分和無界函數的廣義積分;

定積分的應用：幾何應用和物理應用。

7. 空間解析幾何

空間直角坐標系、兩點間的距離公式;

向量及其加減法、向量與數量的乘法、向量的坐標、向量的乘法(數量積、向量積、混合積);

平面、直線方程;

曲面及其方程;

二次曲面;

空間曲線及其方程。

8. 多元函數的微分學

多元函數的概念;

二元函數的極限與連續;

偏導數的概念與二元函數的偏導數的幾何意義;

高階偏導數、高階混合偏導數與求導順序的無關性;

多元復合函數的求導法則;

全微分的概念;

多元函數的極值及其求法;

多元函數的最大、最小值應用問題。

9. 多元函數的積分學

二重積分的定義、性質、計算法(直角坐標、極坐標)。

三重積分的定義、性質、簡單計算。

10. 常微分方程

常微分方程的定義、階、解、通解、初始條件、特解。

可分離變量的微分方程，齊次方程，一階線性方程;

可降階的三種特殊類型的方程：

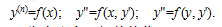
二階線性方程解的結構;

二階常系數齊次線性微分方程;

二階常系數非齊次線性微分方程;

用微分方程解決實際問題。

11. 無窮級數

常數項級數的概念、性質;

正項級數及其審斂準則;

一般項級數及其審斂準則;

冪級數概念、審斂準則、運算性質;

泰勒公式、泰勒級數(麥克勞林級數);

函數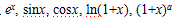的麥克勞林展開式;

函數的泰勒展開(間接)。

參考教材

高等數學(第六版)，同濟大學數學系編。

高等數學(第二版) 宋國華,崔景安 主編, 石油工業出版社。

[注] 現行各種高數教材均可作為備考用書。考試側重于考生對相關內容的掌握程度，不依照某一本教材出題。