軟考初級程序員考什么？軟考初級程序員知識點匯總
1) 進制之間的轉換
進制的種類：二進制(B)、八進制(O)、十進制(D)、十六進制(H)
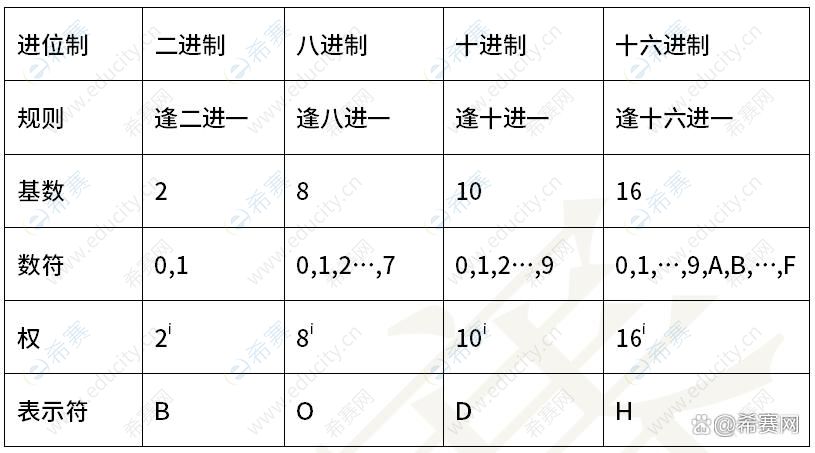
進制的轉化：二進制、八進制、十進制、十六進制之間的相互轉換。
2) 原碼、反碼、補碼和移碼
原碼：將數據用二進制形式表示，最高位為符號位, 正數為0, 負數為1。
反碼：正數的反碼是其本身;負數的反碼是在其原碼的基礎上, 符號位不變，其余各位取反。
補碼：正數的補碼是其本身;負數的補碼是在其原碼的基礎上, 符號位不變, 在反碼的基礎上+1。
移碼：將補碼的符號位取反得相應的移碼。
注意：在補碼和移碼表示中，0有唯一的編碼，補碼中+0和-0均為0000 0000(八位二進制表示下)。
多數計算機都采用補碼進行加減運算，其符號位和數值位一樣參與運算，無須做特殊處理。
在n位二進制表示下：
原碼、反碼表示的數據范圍為：-(2n-1-1)～+(2n-1-1)
補碼、移碼表示的數據范圍為：-2n-1～+(2n-1-1)
補碼中，用1000 0000表示-128。
3) 浮點數表示法
(1)浮點數表示：
N = 數符*尾數m*2階符*階碼e
特點：階碼的位數決定數的表示范圍，位數越多范圍越大;尾數的位數決定數的有效精度，位數越多精度越高
(2)兩浮點數進行運算的過程
運算過程：
對階 > 尾數計算 > 結果格式化
對階時，小數向大數看齊，對階是通過較小數的尾數右移實現的
更多軟考程序員真題點擊下方鏈接獲取~
溫馨提示：因考試政策、內容不斷變化與調整，本網站提供的以上信息僅供參考，如有異議，請考生以權威部門公布的內容為準！
備考學習
一鍵領取新人專享大禮包
備考學習
2025上半年軟考各科真題免費下載
備考學習
系統集成項目管理工程師報考指南視頻課程
備考資料
2025下半年軟考各科模考試卷
歷年真題
軟考各科歷年真題在線答題練習
每日一練
備考2025年軟考不慌，每日一練陪伴你
報考指導
軟考報考指南（全流程詳細指導）
延伸閱讀
軟考備考資料免費領取
去領取
距離考試還有
天
- 1
- 9
- 8
專注在線職業教育24年
APP 
微信群 
掃描二維碼
掃描二維碼
